Today’s article shows you how to double the speed of Math.sqrt, which should be useful to many Flash apps as it is a very common operation. For example, the difference between two points involves a square root: sqrt(dx*dx+dy*dy). Read on to learn how!

For such an important function, I’m surprised there isn’t much out there discussing how to improve its speed. The most informative article on the topic is found at boostworthy.com and lists two alternative functions:

  • The “Babylonian” approach: a loop that gets closer and closer to the actual square root
  • The “Bakhshali” approach: a lookup table where the keys are the squares of the values

The “Babylonian” approach is very accurate, but the “Bakhshali” approach only works on perfect squares (e.g. bakhshali(25)==5 but bakhshali(10)==NaN) due to a divide by zero.

In addition to these approaches, I have added a lookup table-based approach based on a modified version of TrigLUT. This LUT class still supports arbitrary math functions, but has a couple of changes from the TrigLUT class:

  • Uses a max parameter instead of 2π to support square roots up to max
  • Removes all cyclical functions, since Math.sqrt is not cyclical

Here is the source code for the LUT class and a performance test to compare the various approaches:

package
{
	/**
	*   A generic lookup table useful for caching the results of a function
	*   @author Jackson Dunstan
	*/
	public class LUT
	{
		/** Table of function values*/
		public var table:Vector.<Number>;
 
		/** 10^decimals of precision*/
		public var pow:Number;
 
		/**
		*   Make the look up table
		*   @param max Maximum value to cache
		*   @param numDigits Number of digits places of precision
		*   @param func Function to call to generate stored values.
		*               Must be valid on [0,max).
		*   @throws Error If func is null or invalid on [0,max)
		*/
		public function LUT(numDigits:uint, max:Number, func:Function)
		{
			var pow:Number = this.pow = Math.pow(10, numDigits);
			var round:Number = 1.0 / pow;
			var len:uint = 1 + max*pow;
			var table:Vector.<Number> = this.table = new Vector.<Number>(len);
 
			var val:Number = 0;
			for (var i:uint = 0; i < len; ++i)
			{
				table[i] = func(val);
				val += round;
			}
		}
 
		/**
		*   Look up the value of the given input
		*   @param val Input value to look up the value of
		*   @return The value of the given input
		*/
		public function val(val:Number): Number
		{
			return this.table[int(val*this.pow)];
		}
	}
}
package
{
	import flash.display.*;
	import flash.sampler.*;
	import flash.events.*;
	import flash.utils.*;
	import flash.text.*;
	import flash.geom.*;
 
	public class FastSqrtTest extends Sprite
	{
		private var __logger:TextField = new TextField();
		private function log(msg:*): void { __logger.appendText(msg + "\n"); }
 
		private var cache:Object;
 
		public function FastSqrtTest()
		{
			__logger.autoSize = TextFieldAutoSize.LEFT;
			addChild(__logger);
 
			log("Function,Time");
 
			const CACHE_SIZE:int = 10000;
			this.cache = {};
			for (i = 0; i < CACHE_SIZE; ++i)
			{
				this.cache[i * i] = i;
			}
 
			const DIGITS:int = 2;
			var beforeTime:int;
			var afterTime:int;
			var i:int;
			var j:int;
			var result:Number;
			const VAL:Number = 25;
			const REPS:int = 100000;
			const MAX:int = 100;
			const cache:Object = this.cache;
			var lut:LUT = new LUT(DIGITS, MAX, Math.sqrt);
			var lutTable:Vector.<Number> = lut.table;
			var lutPow:Number = lut.pow;
 
			beforeTime = getTimer();
			for(i = 0; i < REPS; ++i)
			{
				for (j = 0; j < MAX; ++j)
				{
					result = Math.sqrt(VAL);
				}
			}
			afterTime = getTimer();
			log("Math.sqrt," + (afterTime - beforeTime));
 
			beforeTime = getTimer();
			for(i = 0; i < REPS; ++i)
			{
				for (j = 0; j < MAX; ++j)
				{
					result = babylonian(VAL);
				}
			}
			afterTime = getTimer();
			log("Babylonian," + (afterTime - beforeTime));
 
			beforeTime = getTimer();
			for(i = 0; i < REPS; ++i)
			{
				for (j = 0; j < MAX; ++j)
				{
					result = bakhshali(VAL);
				}
			}
			afterTime = getTimer();
			log("Bakhshali," + (afterTime - beforeTime));
 
			beforeTime = getTimer();
			for(i = 0; i < REPS; ++i)
			{
				for (j = 0; j < MAX; ++j)
				{
					result = VAL * 0.25;
					var a:Number;
					do
					{
						result = 0.5 * (result + VAL / result);
						a = result * result - VAL;
						if (a < 0) a = -a;
					}
					while (a > 0.0001)
				}
			}
			afterTime = getTimer();
			log("Babylonian (inline)," + (afterTime - beforeTime));
 
			beforeTime = getTimer();
			for(i = 0; i < REPS; ++i)
			{
				for (j = 0; j < MAX; ++j)
				{
					var x:int = int(VAL);
					var y:int = cache[x];
 
					if (y * y == VAL)
					{
						result = y;
					}
					else
					{
						var d:Number = VAL - x;
						var p:Number = d / (y << 2);
						var b:Number = y + p;
 
						result = b - p * p / 2 * b;
					}
				}
			}
			afterTime = getTimer();
			log("Bakhshali (inline)," + (afterTime - beforeTime));
 
			beforeTime = getTimer();
			for(i = 0; i < REPS; ++i)
			{
				for (j = 0; j < MAX; ++j)
				{
					result = lut.val(VAL);
				}
			}
			afterTime = getTimer();
			log("LUT," + (afterTime - beforeTime));
 
			beforeTime = getTimer();
			for(i = 0; i < REPS; ++i)
			{
				for (j = 0; j < MAX; ++j)
				{
					result = lutTable[int(VAL*lutPow)];
				}
			}
			afterTime = getTimer();
			log("LUT (inline)," + (afterTime - beforeTime));
		}
 
		private function babylonian(n:Number): Number
		{
			var x:Number = n * 0.25;
			var a:Number;
			do
			{
				x = 0.5 * (x + n / x);
				a = x * x - n;
				if (a < 0) a = -a;
			}
			while (a > 0.0001)
			return x;
		}
 
		private function bakhshali(n:Number): Number
		{
			var x:int = int(n);
			var y:int = cache[x];
 
			if (y * y == n)
			{
				return y;
			}
 
			var d:Number = n - x;
			var p:Number = d / (y << 2);
			var a:Number = y + p;
 
			return a - p * p / 2 * a;
		}
	}
}

This is the environment I ran the test app on:

  • Flex SDK (MXMLC) 4.1.0.16076, compiling in release mode (no debugging or verbose stack traces)
  • Release version of Flash Player 10.3.181.14
  • 2.4 Ghz Intel Core i5
  • Mac OS X 10.6.7

And here are the results I got:

Function Time
Math.sqrt 219
Babylonian 415
Bakhshali 424
Babylonian (inline) 415
Bakhshali (inline) 354
LUT 163
LUT (inline) 97

Here is the same performance test data in graph form:

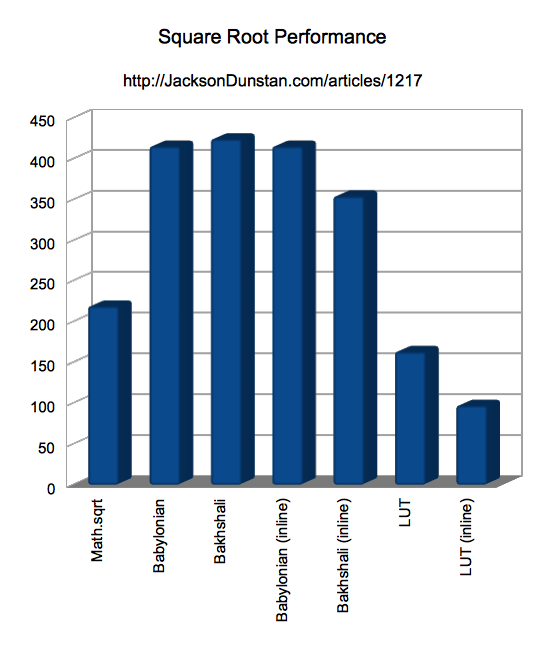
Square Root Performance Graph

From these results we can conclude that:

  • The “Babylonian” and “Bakhshali” approaches are nearly twice as slow as Math.sqrt, even when inlined
  • The LUT class is about 25% faster when used normally and twice as fast when inlined

Speed is useless without accuracy, so let’s have a look at a demo app that plots the square roots from 0 to 100, scaled by a factor of 70 to make it easier to see:

package
{
	import flash.display.*;
	import flash.filters.*;
	import flash.events.*;
	import flash.text.*;
	import flash.geom.*;
 
	[SWF(width=640,height=480,backgroundColor=0xEEEAD9)]
	public class FastSqrtDemo extends Sprite
	{
		private static const TEXT_FORMAT:TextFormat = new TextFormat("_sans", 11);
 
		private static const MAX:int = 10*10;
 
		private static const APPROX_METHODS:Array = [
			["LUT","lut"],
			["Babylonian","babylonian"],
			["Bakhshali","bakhshali"]
		]
 
		private var bmd:BitmapData;
		private var bmdRect:Rectangle;
		private var approxFunc:Function;
 
		private var cache:Object;
		private var sqrtLUT:LUT;
 
		public function FastSqrtDemo()
		{
			stage.scaleMode = StageScaleMode.NO_SCALE;
			stage.align = StageAlign.TOP_LEFT;
 
			const CACHE_SIZE:int = 1+MAX;
			this.cache = {};
			for (var i:int = 0; i < CACHE_SIZE; ++i)
			{
				this.cache[i * i] = i;
			}
			this.sqrtLUT = new LUT(2, CACHE_SIZE, Math.sqrt);
 
			var x:Number;
			var y:Number = 0;
 
			var prompt:TextField = new TextField();
			prompt.y = y;
			prompt.defaultTextFormat = TEXT_FORMAT;
			prompt.htmlText = "<b>Approximation Method:</b>";
			prompt.autoSize = TextFieldAutoSize.LEFT;
			prompt.selectable = false;
			addChild(prompt);
 
			const PAD:Number = 3;
 
			const demo:FastSqrtDemo = this;
			var buttons:Array = [];
			y += prompt.height + PAD;
			for each (var category:Array in APPROX_METHODS)
			{
				var tf:TextField = new TextField();
				tf.mouseEnabled = false;
				tf.defaultTextFormat = TEXT_FORMAT;
				tf.text = category[0];
				tf.autoSize = TextFieldAutoSize.LEFT;
				tf.selectable = false;
				tf.x = tf.y = PAD;
 
				var button:Sprite = new Sprite();
				button.buttonMode = true;
				button.name = category[1];
				button.graphics.beginFill(0xE6E2D1);
				button.graphics.drawRect(0, 0, tf.width+PAD*2, tf.height+PAD*2);
				button.graphics.endFill();
				button.addChild(tf);
				button.addEventListener(
					MouseEvent.CLICK,
					function(ev:MouseEvent): void
					{
						var clickButton:Sprite = ev.currentTarget as Sprite;
						for each (var otherButton:Sprite in buttons)
						{
							otherButton.filters = [new BevelFilter()];
							otherButton.buttonMode = true;
							otherButton.mouseEnabled = true;
						}
						clickButton.filters = [];
						clickButton.buttonMode = false;
						clickButton.mouseEnabled = false;
 
						approxFunc = demo[clickButton.name];
						redraw();
					}
				);
				button.x = PAD;
				button.y = y;
 
				buttons.push(button);
				addChild(button);
 
				y += button.height + PAD;
			}
 
			var about:TextField = new TextField();
			about.defaultTextFormat = TEXT_FORMAT;
			about.y = y;
			about.htmlText = "Black line: Math.sqrt\n"
				+ "Red line: approximation\n"
				+ "Demo by <font color=\"#0071BB\"><a href=\""
				+ "http://jacksondunstan.com/articles/1217"
				+ "\">JacksonDunstan.com</a></font>";
			about.autoSize = TextFieldAutoSize.LEFT;
			about.selectable = false;
			addChild(about);
 
			this.bmd = new BitmapData(stage.stageWidth, stage.stageHeight, false, 0xffffffff);
			this.bmdRect = new Rectangle(0, 0, this.bmd.width, this.bmd.height);
			addChildAt(new Bitmap(bmd), 0);
			buttons[0].dispatchEvent(new MouseEvent(MouseEvent.CLICK));
		}
 
		private function redraw(): void
		{
			var bmd:BitmapData = this.bmd;
			bmd.lock();
			var w:int = bmd.width;
			var h:int = bmd.height;
			bmd.fillRect(this.bmdRect, 0xEEEAD9);
			var halfH:int = h / 2;
			var stepVal:Number = MAX / Number(w);
			var val:Number = 0;
			const SCALE:Number = 70;
			for (var x:int = 0; x < w; ++x)
			{
				bmd.setPixel(
					x,
					h - 1 - Math.sqrt(val)*SCALE,
					0xff000000
				);
				bmd.setPixel(
					x,
					h - 1 - (this.approxFunc(val) || 0)*SCALE,
					0xffff0000
				);
				val += stepVal;
			}
			bmd.unlock();
		}
 
		private function lut(x:Number): Number
		{
			return sqrtLUT.val(x);
		}
 
		private function babylonian(n:Number): Number
		{
			var x:Number = n * 0.25;
			var a:Number;
			do
			{
				x = 0.5 * (x + n / x);
				a = x * x - n;
				if (a < 0) a = -a;
			}
			while (a > 0.0001)
			return x;
		}
 
		private function bakhshali(n:Number): Number
		{
			var x:int = int(n);
			var y:int = cache[x];
 
			if (y * y == n)
			{
				return y;
			}
 
			var d:Number = n - x;
			var p:Number = d / (y << 2);
			var a:Number = y + p;
 
			return a - p * p / 2 * a;
		}
	}
}

Demo

This demo makes it plain that the LUT and “Babylonian” methods are very accurate, but the “Bakhshali” method is useless (returning NaN) everywhere but the perfect squares.

In conclusion, an inlined version of the LUT class is twice as fast as Math.sqrt. It’s only one line of code to inline and doesn’t use very much memory, so why not double your square root speed?

Know of any more ways to speed up square roots? Post a comment below!