Floating-point math is fast these days, but fixed-point still has a purpose: we can use it to store real numbers in less than 32 bits. Saving a measly 16 or 24 bits off a float might not sound appealing, but cutting the data size in half or quarter often does when multiplied across large amounts of real numbers. We can shrink downloads, improve load times, save memory, and fit more into the CPU’s data caches. So today we’ll look at storing numbers in fixed-point formats and see how easy it can be to shrink our data!

Formats

Like floating-point, fixed-point is a family of formats. Floating point has 32-bit (float) and 64-bit (double) variants, but fixed-point has many more possibilities. It’s appealing because we get to decide how many bits to use and how to allocate them on our particular data, not data in general. For example, if we have percentages then we might choose this 8-bit format:

0 1 2 3 4 5 6 7
W F F F F F F F

W represents a bit storing the whole number and F represents a bit storing a fractional number.

In this case, the whole number can only be 0 or 1. That’s OK because percentages are only from 0.0 to 1.0. The remaining seven bits are all for the fractional part. This number is an integer between 0 and 127 (27-1). When converting to a float, the whole number is added to 1/Fraction to get the result. That means the fraction has a precision of 1/127 or about 0.007874015748.

For many uses, this is plenty of precision. If not, we can always increase the size to 16 bits and store the fraction in 15 bits:

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
W F F F F F F F F F F F F F F F

This increases the maximum to 32767 (215-1) so the precision is now 1/32767 or about 0.00003051850948. That’s enough for most purposes.

Another option when designing a fixed-point format is to add a sign bit so we can represent negative numbers. Say we have a character creation tool where users can shift the skeleton’s facial joints to personalize the character. We might design a format like this:

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
S W W W W W W W W F F F F F F F

S represents the sign bit. There are 8 whole bits and 7 fractional bits. This means the user can move the joints up to 255 (28-1) millimeters (10.03937 inches) with a precision, again, of 0.007874015748 millimeters (0.00031000062 inches). That’s probably good enough for normal faces.

Types

Now let’s look at how we can make a fixed-point format in C#. Thankfully, structs and operator overloading make this quite simple. We can use the pattern set down in the Unity.Mathematics package with types like half to create our own formats. Here’s one named fixed8_8 because it has 8 whole bits and 8 fraction bits:

using System;
using System.Runtime.CompilerServices;
 
public struct fixed8_8 : IEquatable<fixed8_8>, IFormattable
{
    private const int One = 0x100;
 
    public short value;
 
    /// <summary>fixed10_6 zero value.</summary>
    public static readonly fixed8_8 zero = new fixed8_8();
 
    public static float MaxValue
    {
        get { return 127.9961f; }
    }
 
    public static float MinValue
    {
        get { return -128.0f; }
    }
 
    /// <summary>Constructs a fixed10_6 value from a fixed10_6 value.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public fixed8_8(fixed8_8 x)
    {
        value = x.value;
    }
 
    /// <summary>Constructs a fixed10_6 value from a float value.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public fixed8_8(float v)
    {
        value = FromFloat(v);
    }
 
    /// <summary>Constructs a fixed10_6 value from a double value.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public fixed8_8(double v)
    {
        value = FromFloat((float)v);
    }
 
    /// <summary>Explicitly converts a float value to a fixed10_6 value.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static explicit operator fixed8_8(float v)
    {
        return new fixed8_8(v);
    }
 
    /// <summary>Explicitly converts a double value to a fixed10_6 value.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static explicit operator fixed8_8(double v)
    {
        return new fixed8_8(v);
    }
 
    /// <summary>Implicitly converts a fixed10_6 value to a float value.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static implicit operator float(fixed8_8 d)
    {
        return ToFloat(d.value);
    }
 
    /// <summary>Implicitly converts a fixed10_6 value to a double value.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static implicit operator double(fixed8_8 d)
    {
        return ToFloat(d.value);
    }
 
 
    /// <summary>Returns whether two fixed10_6 values are equal.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static bool operator ==(fixed8_8 lhs, fixed8_8 rhs)
    {
        return lhs.value == rhs.value;
    }
 
    /// <summary>Returns whether two fixed10_6 values are different.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static bool operator !=(fixed8_8 lhs, fixed8_8 rhs)
    {
        return lhs.value != rhs.value;
    }
 
 
    /// <summary>Returns true if the fixed10_6 is equal to a given fixed10_6, false otherwise.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public bool Equals(fixed8_8 rhs)
    {
        return value == rhs.value;
    }
 
    /// <summary>Returns true if the fixed10_6 is equal to a given fixed10_6, false otherwise.</summary>
    public override bool Equals(object o)
    {
        return Equals((fixed8_8)o);
    }
 
    /// <summary>Returns a hash code for the fixed10_6.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public override int GetHashCode()
    {
        return value;
    }
 
    /// <summary>Returns a string representation of the fixed10_6.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public override string ToString()
    {
        return ToFloat(value).ToString();
    }
 
    /// <summary>Returns a string representation of the fixed10_6 using a specified format and culture-specific format information.</summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public string ToString(string format, IFormatProvider formatProvider)
    {
        return ToFloat(value).ToString(format, formatProvider);
    }
 
    private static float ToFloat(short val)
    {
        return ((float)val) / One;
    }
 
    private static short FromFloat(float val)
    {
        return (short)(val * One);
    }
}
 
namespace Unity.Mathematics
{
    public static partial class math
    {
        /// <summary>Returns a fixed10_6 value constructed from a fixed10_6 values.</summary>
        [MethodImpl(MethodImplOptions.AggressiveInlining)]
        public static fixed8_8 fixed10_6(fixed8_8 x)
        {
            return new fixed8_8(x);
        }
 
        /// <summary>Returns a fixed10_6 value constructed from a float value.</summary>
        [MethodImpl(MethodImplOptions.AggressiveInlining)]
        public static fixed8_8 fixed10_6(float v)
        {
            return new fixed8_8(v);
        }
 
        /// <summary>Returns a fixed10_6 value constructed from a double value.</summary>
        [MethodImpl(MethodImplOptions.AggressiveInlining)]
        public static fixed8_8 fixed10_6(double v)
        {
            return new fixed8_8(v);
        }
 
        /// <summary>Returns a uint hash code of a fixed10_6 value.</summary>
        [MethodImpl(MethodImplOptions.AggressiveInlining)]
        public static uint hash(fixed8_8 v)
        {
            return (ushort)v.value * 0x745ED837u + 0x816EFB5Du;
        }
    }
}

Most of this code is boilerplate, but there are some intersting parts to call out. First, public short value is the only field. This means the struct has its size: 16 bits. Next, we have private const int One = 0x100 to define what 1.0 looks like. This is equivalent to binary 0000000100000000 meaning the sign bit is 0 (positive in this format), the high whole bits are 0000001 (the 1. part), and the low fraction bits are 00000000 (the .0 part).

The real work happens in ToFloat and FromFloat. All we need to do is multiply or divide by the One value. The nature of the signed short type we used for value and the conversion to and from float takes care of the tricky math for us.

To use the format, all we need to do is cast:

float a = 3.14f;
fixed8_8 b = (fixed8_8)a; // Convert to fixed-point
float c = b; // Convert to floating-point
Testing

To confirm our fixed8_8 type works well, let’s write a little test script. We’ll simply iterate in steps of 0.1 from the minimum value to the maximum value, converting from float to fixed8_8 and back, then printing the delta. In the end we’ll copy this to the clipboard and paste it into a CSV file.

using UnityEditor;
using UnityEngine;
 
class TestScript : MonoBehaviour
{
   void Start()
   {
       string report = "";
       report += "Value,Fixed,Recovered,Errorn";
       for (float v = fixed8_8.MinValue; v <= fixed8_8.MaxValue; v += 0.1f)
       {
           fixed8_8 f = (fixed8_8)v;
           float r = f;
           float e = r - v;
           report +=
               v
               + "," + f.value
               + "," + r
               + "," + e.ToString("F99").TrimEnd('0')
               + "n";
       }
       EditorGUIUtility.systemCopyBuffer = report;
   }
}

Running this gives a lot of rows that look like this when graphed:

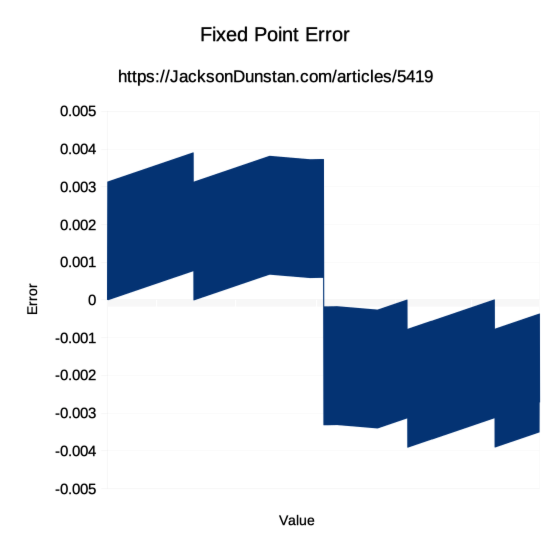
fixed8_8 Error Graph

There’s not enough resolution in the graph to see the individual data points, but we can see the big picture. Negative values have errors between 0 and 0.003898621 while positive values have errors between 0 and -0.003902435. The error rate is uneven, apparently in a sawtooth pattern as it builds up and then suddenly drops when a threshold is reached. Even at the maximum though, the error is only about 0.003898621/128 or 0.003045797656%. Whether this is acceptable or not depends on the data its representing.

To get a better idea of how the error fluctuates, let’s zoom in by looking at just the lowest 10 values:

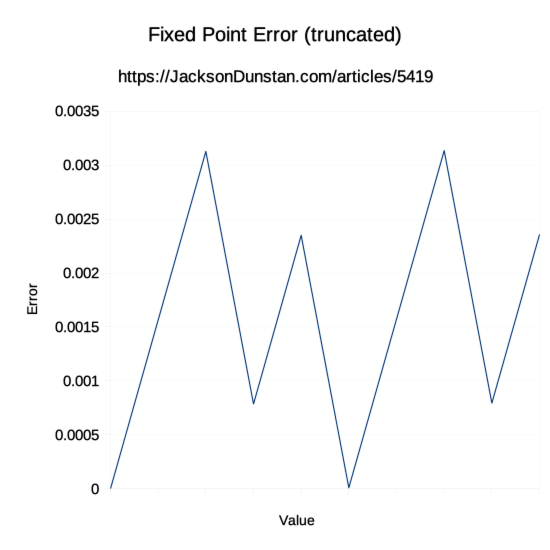
fixed8_8 Error Graph (Truncated)

Here we see fluctuations that span most of the entire 0-0.004 range. They go up to 0.003135681 and all the way down to zero. So there’s quite a lot of error fluctuation even within numbers that are close to each other. Still, it is of course always less than or equal to the total fluctuation of about 0.003045797656%.

Conclusion

Fixed-point numbers are a powerful way to save data space in CPU data caches, install sizes, disk space, and RAM. Sizes shrink by 2x or even 4x. Correspondingly, load times in downloads and level loads will improve as less data needs to be transfered. We can do this with just a little work to design custom formats for our specific data and to create custom C# structs to match. The results retain good precision, performance, and usability.