JacksonDunstan.com

Last week we took a look at function pointers in Burst 1.2 and Unity 2019.3. Today we’ll continue looking into them by analyzing their performance.

Today’s test is tricky to set up due to the nature of modern CPUs. They include very good branch predictors that can mitigate both the overhead of function calls through pointers as well as control flow mechanisms like if. For this reason, we’ll set up four variants of the test to show a range of circumstances in which function pointers might be used.

All of the tests will loop over two arrays of float values, perform either a multiply or divide on them, and store the result in a third array. That middle step that decides which operation to perform is what we’ll vary across the tests. Here are the four variants:

Always divide
Always multiply
Alternate between division and multiplication
50% random chance to divide, 50% random chance to multiply

The major attraction of using function pointers in the first place is that only one job needs to be written:

[BurstCompile]
struct FunctionPointerJob : IJob
{
    [ReadOnly] public NativeArray<FunctionPointer<BinaryFunction>> Funcs;
    [ReadOnly] public NativeArray<float> A;
    [ReadOnly] public NativeArray<float> B;
    [WriteOnly] public NativeArray<float> Sum;
 
    public void Execute()
    {
        for (int i = 0; i < A.Length; ++i)
        {
            Sum[i] = Funcs[i].Invoke(A[i], B[i]);
        }
    }
}

The function pointers in Funcs is a data input to the job and it can be filled with any pattern of function pointers the user of the job desires. It’s not even limited to just division and multiplication. Any function pointer that satisfies the signature of BinaryFunction by taking two float parameters and returning a float can be swapped in. This leads to code reuse and the avoidance of code duplication, both generally considered very positive outcomes.

The non-function pointer variants require four different job types. For brevity, here are just their loop bodies:

// DirectDivideJob
Sum[i] = A[i] / B[i];
 
// DirectMultiplyJob
Sum[i] = A[i] * B[i];
 
// DirectAlternatingJob
if ((i & 1) == 0)
{
    Sum[i] = A[i] / B[i];
}
else
{
    Sum[i] = A[i] * B[i];
}
 
// DirectRandomJob (with Unity.Mathematics.Random Rand field)
if (Rand.NextBool())
{
    Sum[i] = A[i] / B[i];
}
else
{
    Sum[i] = A[i] * B[i];
}

Will the code duplication pay off? Let’s find out by putting them to the test with the following script:

using System.Diagnostics;
using UnityEngine;
using Unity.Burst;
using Unity.Collections;
using Unity.Jobs;
 
delegate float BinaryFunction(float a, float b);
 
[BurstCompile]
public static class BinaryFunctions
{
    [BurstCompile]
    public static float Divide(float a, float b)
    {
        return a / b;
    }
 
    [BurstCompile]
    public static float Multiply(float a, float b)
    {
        return a * b;
    }
}
 
[BurstCompile]
struct FunctionPointerJob : IJob
{
    [ReadOnly] public NativeArray<FunctionPointer<BinaryFunction>> Funcs;
    [ReadOnly] public NativeArray<float> A;
    [ReadOnly] public NativeArray<float> B;
    [WriteOnly] public NativeArray<float> Sum;
 
    public void Execute()
    {
        for (int i = 0; i < A.Length; ++i)
        {
            Sum[i] = Funcs[i].Invoke(A[i], B[i]);
        }
    }
}
 
[BurstCompile]
struct DirectRandomJob : IJob
{
    public Unity.Mathematics.Random Rand;
    [ReadOnly] public NativeArray<float> A;
    [ReadOnly] public NativeArray<float> B;
    [WriteOnly] public NativeArray<float> Sum;
 
    public void Execute()
    {
        for (int i = 0; i < A.Length; ++i)
        {
            if (Rand.NextBool())
            {
                Sum[i] = A[i] / B[i];
            }
            else
            {
                Sum[i] = A[i] * B[i];
            }
        }
    }
}
 
[BurstCompile]
struct DirectAlternatingJob : IJob
{
    [ReadOnly] public NativeArray<float> A;
    [ReadOnly] public NativeArray<float> B;
    [WriteOnly] public NativeArray<float> Sum;
 
    public void Execute()
    {
        for (int i = 0; i < A.Length; ++i)
        {
            if ((i & 1) == 0)
            {
                Sum[i] = A[i] / B[i];
            }
            else
            {
                Sum[i] = A[i] * B[i];
            }
        }
    }
}
 
[BurstCompile]
struct DirectDivideJob : IJob
{
    [ReadOnly] public NativeArray<float> A;
    [ReadOnly] public NativeArray<float> B;
    [WriteOnly] public NativeArray<float> Sum;
 
    public void Execute()
    {
        for (int i = 0; i < A.Length; ++i)
        {
            Sum[i] = A[i] / B[i];
        }
    }
}
 
[BurstCompile]
struct DirectMultiplyJob : IJob
{
    [ReadOnly] public NativeArray<float> A;
    [ReadOnly] public NativeArray<float> B;
    [WriteOnly] public NativeArray<float> Sum;
 
    public void Execute()
    {
        for (int i = 0; i < A.Length; ++i)
        {
            Sum[i] = A[i] * B[i];
        }
    }
}
 
class TestScript : MonoBehaviour
{
    void Start()
    {
        const int len = 1000000;
        NativeArray<FunctionPointer<BinaryFunction>> funcs =
            new NativeArray<FunctionPointer<BinaryFunction>>(
                len,
                Allocator.TempJob);
        NativeArray<float> a = new NativeArray<float>(len, Allocator.TempJob);
        NativeArray<float> b = new NativeArray<float>(len, Allocator.TempJob);
        NativeArray<float> sum = new NativeArray<float>(len, Allocator.TempJob);
        FunctionPointer<BinaryFunction> divide =
            BurstCompiler.CompileFunctionPointer<BinaryFunction>(
                BinaryFunctions.Divide);
        FunctionPointer<BinaryFunction> multiply =
            BurstCompiler.CompileFunctionPointer<BinaryFunction>(
                BinaryFunctions.Multiply);
        for (int i = 0; i < funcs.Length; ++i)
        {
            if (UnityEngine.Random.Range(0, 2) == 0)
            {
                funcs[i] = divide;
            }
            else
            {
                funcs[i] = multiply;
            }
        }
        FunctionPointerJob fpJob = new FunctionPointerJob
        {
            Funcs = funcs,
            A = a,
            B = b,
            Sum = sum
        };
        DirectRandomJob directRandomJob = new DirectRandomJob
        {
            Rand = new Unity.Mathematics.Random(
                (uint)UnityEngine.Random.Range(int.MinValue, int.MaxValue)),
            A = a,
            B = b,
            Sum = sum
        };
        DirectAlternatingJob directAlternatingJob = new DirectAlternatingJob
        {
            A = a,
            B = b,
            Sum = sum
        };
        DirectDivideJob directDivideJob = new DirectDivideJob
        {
            A = a,
            B = b,
            Sum = sum
        };
        DirectMultiplyJob directMultiplyJob = new DirectMultiplyJob
        {
            A = a,
            B = b,
            Sum = sum
        };
 
        // Warmup
        fpJob.Run();
        directAlternatingJob.Run();
        directDivideJob.Run();
        directMultiplyJob.Run();
 
        Stopwatch sw = Stopwatch.StartNew();
        fpJob.Run();
        long fpRand = sw.ElapsedTicks;
 
        for (int i = 0; i < funcs.Length; ++i)
        {
            if ((i & 1) == 0)
            {
                funcs[i] = divide;
            }
            else
            {
                funcs[i] = multiply;
            }
        }
 
        sw.Restart();
        fpJob.Run();
        long fpAlt = sw.ElapsedTicks;
 
        for (int i = 0; i < funcs.Length; ++i)
        {
            funcs[i] = divide;
        }
 
        sw.Restart();
        fpJob.Run();
        long fpDiv = sw.ElapsedTicks;
 
        for (int i = 0; i < funcs.Length; ++i)
        {
            funcs[i] = multiply;
        }
 
        sw.Restart();
        fpJob.Run();
        long fpMul = sw.ElapsedTicks;
 
        sw.Restart();
        directRandomJob.Run();
        long dirRand = sw.ElapsedTicks;
 
        sw.Restart();
        directAlternatingJob.Run();
        long dirAlt = sw.ElapsedTicks;
 
        sw.Restart();
        directDivideJob.Run();
        long dirDiv = sw.ElapsedTicks;
 
        sw.Restart();
        directMultiplyJob.Run();
        long dirMul = sw.ElapsedTicks;
 
        funcs.Dispose();
        a.Dispose();
        b.Dispose();
        sum.Dispose();
 
        print(
            "Choice,Random,Alternating,Always Divide,Always Multiplyn" + 
            $"Function Pointer,{fpRand},{fpAlt},{fpDiv},{fpMul}n" +
            $"Direct,{dirRand},{dirAlt},{dirDiv},{dirMul}");
    }
}

I ran the test in this environment:

2.7 Ghz Intel Core i7-6820HQ
macOS 10.15.3
Unity 2019.3.3f1
macOS Standalone
.NET 4.x scripting runtime version and API compatibility level
IL2CPP
Non-development
640Ã—480, Fastest, Windowed

And here are the results I got:

Choice	Random	Alternating	Always Divide	Always Multiply
Function Pointer	75724	32779	31925	31963
Direct	75288	12316	6172	6092

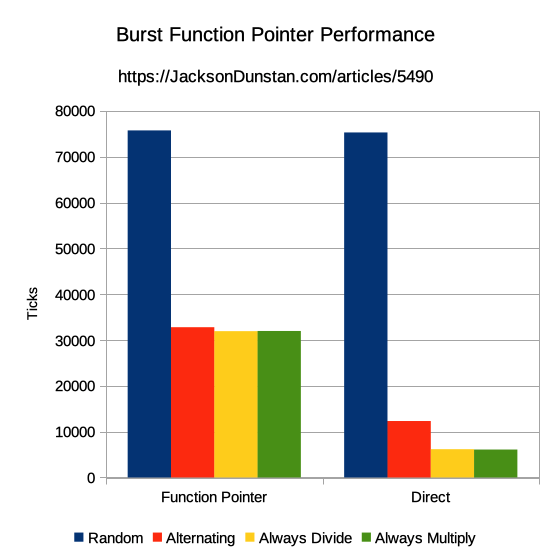
Burst Function Pointer Performance Graph

First off, we see that random operations are the slowest of all and nearly identical in performance between both approaches. This is the case designed to fool the CPU’s branch predictor because there isn’t any pattern to the control flow. The times are nearly identical, but the work being done is quite different. In the function pointer approach, it’s loading the address of the function and jumping there. In the direct approach, it’s calling Random.NextBool which looks like this in com.unity.mathematics version 1.1.0:

[MethodImpl(MethodImplOptions.AggressiveInlining)]
private uint NextState()
{
    CheckState();
    uint t = state;
    state ^= state << 13;
    state ^= state >> 17;
    state ^= state << 5;
    return t;
}
 
[Conditional("ENABLE_UNITY_COLLECTIONS_CHECKS")]
private void CheckState()
{
#if ENABLE_UNITY_COLLECTIONS_CHECKS
    if(state == 0)
        throw new System.ArgumentException("Invalid state 0. Random object has not been properly initialized");
#endif
}

CheckState is removed at compile time, so it’s not taking any time. The remaining work is three shift and three exclusive-or operations. Those are very fast instructions, so this isn’t much work. The fact that the function pointer approach executes just as quickly, shows roughly how much it costs when the branch predictor can’t accurately predict where to go: these six instructions.

Next, we see that the times drop in the alternating operations case for both function pointers and the direct approach. The function pointer time dropped 57% and the direct approach dropped 84%. The single bitwise and operation and if conditional are 2.7x faster than the function pointer.

Finally, we have the “always divide” and “always multiply” cases. These times are slightly better for the function pointer approach than the alternating operations case. Because it dropped so little, this shows that the CPU is usually capable of correctly predicting which function will need to be called in the alternating operations case because the pattern is simple enough. In the direct approach, the time was cut in half compared to the alternating case, resulting in the lowest overall times: over 10x faster than the random operations case.

There are some things to keep in mind about these results. First, CPU branch predictors are specific to the CPU. Running this test on an ARM or AMD processor may yield very different results. As always, it’s a good idea to test on the hardware the game is expected to run on for the most accurate results.

Second, the function pointer results essentially represent two tiers: unpredictable and predictable. The results will always be somewhere between the results for random and the results for divide and multiply. This is because the work to decide which operation to perform was done before the job even ran. That result of that work is then stored in function pointers and may be used and reused as long as it remains valid.

On the contrary, the direct approach performs the decision work every time the job is run and in every iteration of the loop. The cost of that work will scale with its complexity. If the same decisions are repeatedly used, the total time used by the function pointer approach will be less than the total time used by the direct approach even if the direct approach is faster for one run of the job. It’s important to know the work the game is doing in terms of recalculating those decisions, reusing them, and the cost of deciding in order to choose the fastest approach.

The bottom line is that function pointers aren’t simply faster or slower than the direct approach. They may be either, or even equal.

#1 by Henke37 on March 9th, 2020 · Reply

I propose the theory that the branch predictor may work differently if there are more than two possibilities. Further research is required.

#2 by jackson on March 9th, 2020 · Reply

Oh, definitely. Any given modern branch predictor is very complicated and may even involve machine learning . You could spend a lot of time researching them.

#3 by Shachar Langbeheim on March 9th, 2020 · Reply

” This is because the work to decide which operation to perform was done before the job even ran. […] the direct approach performs the decision work every time the job is run and in every iteration of the loop.”

That’s an implementation detail. You could’ve just as easily pre-computed the decisions and saved them in an array of bools for the direct approach, and gotten better performance.

#4 by jackson on March 9th, 2020 · Reply

That sentence was specifically talking only about the test that was actually run in the article. It’s hard to know if alternative tests that weren’t part of the article such as the one you suggest would result in better performance. If you write it, please post your results here.

Burst Function Pointers Performance

Comments